Errors are an unavoidable phenomenon in computation, and this is especially true in quantum computation, where we must exercise precise control over the behavior of ultra-sensitive quantum systems. While we look for computational advantage in the near term by using techniques that reduce the effects of noise in quantum systems, extracting the full potential of computation and realizing quantum algorithms with a super-polynomial speedup will most likely require major advances in quantum error correction technology.1
Researchers in the field have made significant progress in quantum error correction over the last few years, but there's still much left to accomplish to achieve this goal. Today, we’re working with the broader quantum community to thoughtfully bring about practical quantum computing as soon as possible. As part of our development roadmap, we see the development in this field as a continuous path forward, where we work to create value from today’s noisy quantum hardware using error mitigation techniques
With fault tolerance the ultimate goal, error mitigation is the path that gets quantum computing to usefulness. Read more.
Our ultimate challenge is to design quantum error correction technologies that enable the construction of fault tolerant quantum computers — that is quantum computers that can detect and correct errors faster than errors occur.
We see the development in this field as a continuous path forward, where we work to create value from today’s noisy quantum hardware using error mitigation techniques.
Research is still underway to bring the world into an era of fault-tolerant quantum computation. However, the field is advancing quickly, and the community has overcome some of the major challenges that have long plagued its development. IBM Quantum is deeply committed to participating in this community to advance error correction technology. IBM research in error correction and its hosting events like the Quantum Error Correction Summer School have allowed us to help foster novel ideas that will bring us closer to being able to perform arbitrarily long, error-free quantum calculations. We are beginning to see the path forward toward the era of fault tolerance.
What is quantum error correction?
The modern world relies on the storage, transmission, and processing of digital information — information represented as 0s and 1s called bits. Occasionally, digital information becomes corrupted or damaged when some of these bits flip from a 0 to a 1, or from a 1 to a 0. Conventional classical computers are highly reliable under these conditions because modern computer components experience these errors rarely, and because error correction schemes protect the storage and transmission of data.
On the other hand, quantum computers, which use qubits instead of 0s and 1s
How to fix quantum computing bugs? Read IBM quantum theorist Dr. Zaira Nazario’s article about how the same physics that makes quantum computers powerful also makes them finicky. New techniques aim to correct errors faster than they can build up.
Quantum error correction codes provide the protection needed for quantum computers to operate reliably in the presence of these much higher error rates and wider set of error types. Crucially, these codes must work without directly measuring data qubits, since that measurement would cause a quantum processor to lose its quantum information and hence lose the advantages of quantum computing.
There are many possible error-correcting codes that could be useful for a variety of contexts. The most promising family of codes at this time are called quantum Low-Density Parity Check (qLDPC) codes — codes which diagnose quantum errors by performing certain checks on a few qubits, and where each qubit participates in a few checks. These checks are analogous to parity checks in classical error correction.
The fact that these tests require only a few physical qubits makes qLDPC codes highly appealing when it comes to designing efficient quantum circuits for error correction, since a faulty operation in the circuit would damage the state only of those few physical qubits that participate in the same parity check. Important codes such as the 2D surface codes and 2D color codes, with which many current experiments are performed today, all belong to the qLDPC family.
Error correction as benchmarking
Making reliable quantum computers at scale is difficult. It is therefore necessary to study and implement codes on today’s hardware, not only to expand our knowledge of how to engineer better quantum computers, but also to help benchmark the state of current hardware. This helps refine our understanding of system-level requirements and improve our systems’ capabilities. By pushing these capabilities to their physical limits, and evaluating them with well-designed benchmarks, the research community discovers important constraints that inform us how to co-design optimal protocols for error suppression, mitigation, and correction during quantum computations. Therefore, a lot of present QEC research goes into experimental demonstrations that use the most suitable QEC codes available to implement logical operations on today’s quantum hardware.
Many of these demonstrations involve researchers implementing surface code and related heavy-hexagon code2 schemes. These code families are designed for use on a two-dimensional lattice of qubits, typically featuring physical qubits with various roles: data qubits for storing data and auxiliary qubits for measuring checks or flags. We measure the robustness of these codes to errors via “distance,” a metric representing the minimum number of physical qubit errors required to return an incorrect logical qubit value. Thus, increasing the distance implies a more robust code. The probability of a logical qubit error decreases exponentially as distance increases.
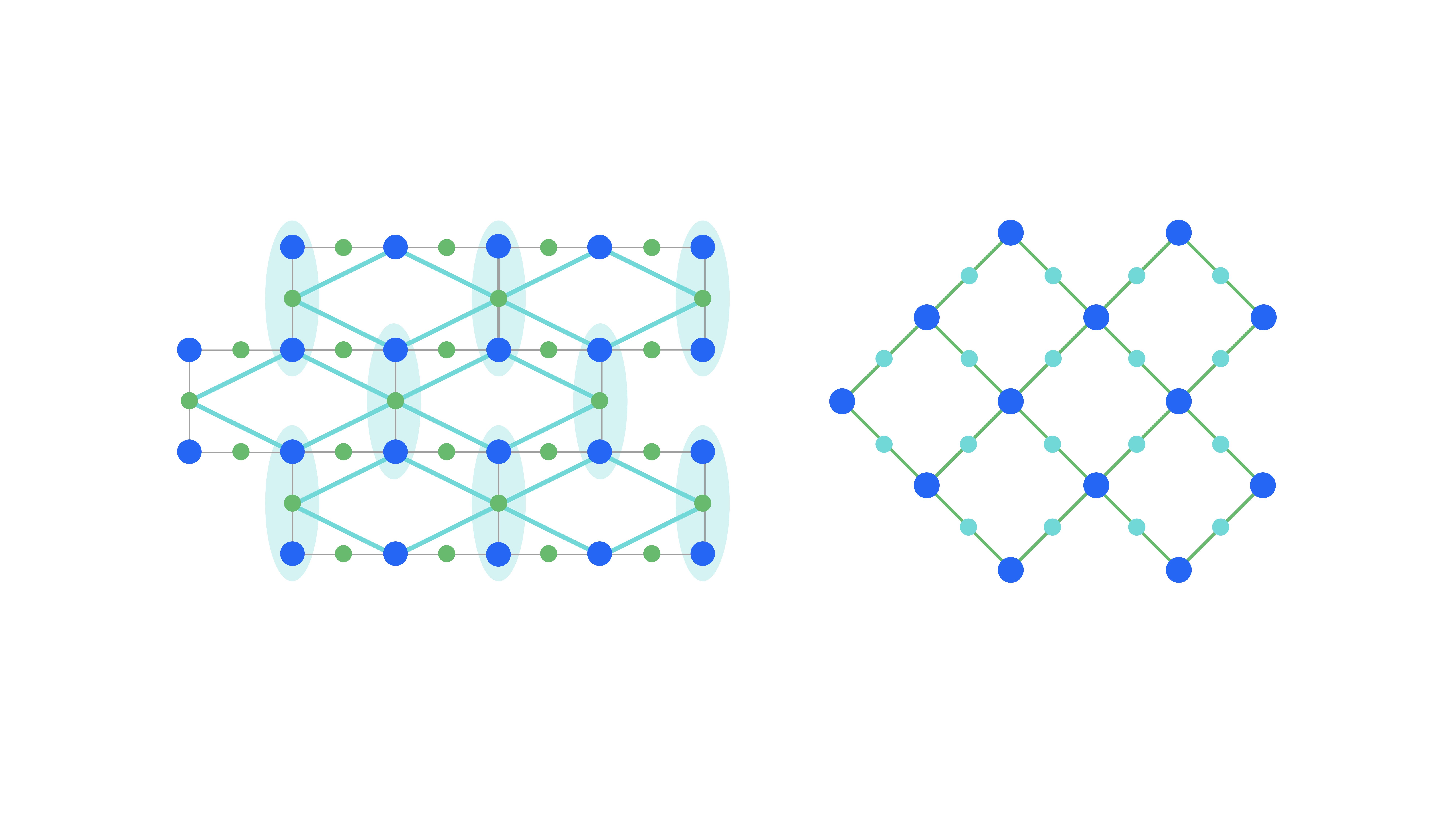
Encoding into the 3-qubits repetition code (left) leads to a logical heavy square lattice (right).
This past year, we’ve seen implementations of distance 23 and distance 34 codes at IBM, an implementation of a distance 3 code5 from researchers at ETH-Zurich, and even the implementation of a distance 5 code6 from researchers at Google. These codes represent important experimental work, perhaps most importantly because the fact that we can implement these codes at all shows just how much progress we’ve made toward reducing errors in our quantum processors. Additionally, measuring improvements in logical error rates will provide further evidence (and perhaps a confidence boost) that the field is on the right track.
Other teams have presented experimental demonstrations of other kinds of error correcting codes, called color codes. Color codes and surface codes follow similar principles, but color codes have simpler quantum logical gates at the expense of larger parity checks. Last year, researchers at Honeywell (now Quantinuum) implemented a color code on their trapped ion hardware. This year, researchers at the University of Innsbruck implemented the critically important T-gate7 as part of a color code demonstration, while researchers at Quantinuum implemented an error-corrected CNOT gate,8 which is one of the gates that provide entanglement. As with the surface code examples, these demonstrations help draw a line in the sand representing the current state-of-the-art for error correction, while signaling a way forward when working to improve these codes.
Developing new codes
The 2D surface code has so far been considered an uncontested leader in terms of the error correction — yet it has two important shortcomings. First, most physical qubits are devoted to error correction. As the distance of the surface code grows, the number of physical qubits must grow like the square of the distance, all to encode a single qubit. For example, a distance-10 surface code would need approximately 200 physical qubits to encode one logical qubit. Second, it is difficult to implement a computationally universal set of logical gates. The leading approach, called magic state distillation, requires additional resources beyond simply encoding quantum information into error correcting codes. The space-time cost of these additional resources may be prohibitively expensive for small or medium size computations.1
One approach to solving the first shortcoming of the surface code is to find and study codes from “good” families of qLDPC codes. “Good” is a technical term (of course we want good codes in the colloquial sense). A good code family is one where the number of logical qubits and the distance scale proportionally with the number of physical qubits, so that doubling the physical qubits would double both the number of logical qubits and the distance. The surface code family is not “good,” and finding good qLDPC codes has been a major open question in quantum error correction.
A significant advance toward this question came in 2009, when researchers Jean-Pierre Tillich and Gilles Zémor uncovered a family of codes called hypergraph product codes.9 These codes did not improve the square root distance limit, but they did dramatically improve the scaling of physical qubits to logical qubits. Last year brought a landmark paper10 from Pavel Panteleev and Gleb Kalachev at Moscow State University offering an ingenious mathematical proof of a recent conjecture11 by Nikolas Breuckmann and Jens Eberhardt that there exists a class of qLDPC codes — called lifted (or balanced) product codes — which could break this barrier. In other words, they discovered good families of codes. Unlike the surface code though, these new qLDPC codes need more qubit connectivity than a two-dimensional lattice provides, that is, some qubits need to be connected over long distances.
Together, these discoveries have opened new directions in quantum error correction and led to further developments. For example, earlier this year, Anthony Leverrier and Gilles Zémor published12 a simplified version of the Panteleev and Kalachev code, called a quantum Tanner code, which tightened our understanding of these codes' capabilities. This past summer, researchers from MIT and Caltech debuted an efficient decoder13 for quantum Tanner codes — a crucial step for making these next-generation codes a reality.
Good qLDPC codes are one possible approach toward efficient fault-tolerant quantum computing. Other approaches have the potential to solve the second shortcoming of the surface code by making universal logical gates less expensive. A team led by IBM Quantum’s Guanyu Zhu investigated a class of codes called Fractal Surface Codes 14 (FSCs), which are 3D codes constructed by punching holes with smooth boundaries in the 3D surface code such that the resulting lattice is a fractal. Like qLDPC codes, FSCs combine multiple physical qubits together to simulate some underlying topological order (i.e., logical qubits) and conserve some basic properties of the system even in the presence of small perturbations. However, also like qLDPC codes, they require more complex qubit connections than a two-dimensional lattice. The benefit is a code that requires much less overhead to implement a universal set of logical gates.
There are other codes in the pipeline as well. Last year, researchers at Microsoft debuted the honeycomb code,15 so named because it organizes qubits on the vertices of a hexagonal lattice. This is like, but not the same as the heavy hexagon code used by IBM Quantum today. The key difference between a honeycomb code and a 2D surface code is that the logical qubits are dynamically defined (a logical qubit doesn't necessarily correspond to the exact same physical qubits over the course of the calculation) and the checks can be measured with incredibly simple quantum circuits. At the time of this writing, the honeycomb code has only been shown to be competitive with leading planar codes by performing what is called entangling measurements (measuring two qubits simultaneously in a way that preserves their entanglement) of the parity checks.
In a follow-up paper,16 researchers at Google and the University of Santa Barbara benchmarked the honeycomb code, and found that it would require 7,000 physical qubits to encode a single logical qubit with a one-in-a-trillion logical error rate. They concluded that this code was a promising candidate for implementing error correction on today's quantum hardware with its two-dimensional qubit lattices.
Decoding
When we perform quantum computations with a deployed error correction code, we observe non-trivial error-sensitive events—these events are clues to what the underlying errors are, and when they occur, it is then the task of the decoder to correctly identify suitable corrections. Classical hardware performs this decoding and must keep pace with the high rate at which nontrivial events occur. Further, the amount of event data transferred from the quantum device to the classical hardware must not exceed the available bandwidth. Decoders therefore place additional constraints on the control hardware and on the way quantum computers interface with classical systems. Solving this challenge is of key importance both theoretically and experimentally.
Decoders for many types of codes are computationally efficient (i.e., run in polynomial time) however this may not be sufficient given the above constraints. Developing and experimenting with real-time decoders is becoming an important aspect of creating a useful quantum system. This fact was evident from the real-time decoder session that took place at the recent IEEE Quantum week event in Denver, Colorado, and from the number of recent papers on real-time decoders from IBM, AWS, Quantinuum, and others.
Research continues within the community to develop better decoders and to understand the underlying reasons why they work. For general stabilizer codes, IBM’s Ben Brown has been recently exploiting the underlying structure that arises due to symmetries among surface-code stabilizer elements. By concentrating on these symmetries, he has begun to address the question of how a decoder called the minimum-weight perfect-matching decoder might be generalized for other types of codes.17
Earlier this year, a team of IBM researchers implemented and demonstrated decoders called matching and maximum likelihood decoders18 for distance-2 and -3 heavy hex codes on IBM Quantum hardware — with the help of mid-circuit measurement and fast reset. These are but some of the important research results on decoders that have appeared recently, and many more exciting results are expected in the future.
Performing calculations
One can’t simply encode and decode logical qubits; however, we must also be able to perform calculations with them. Therefore, a key challenge is to find simple, inexpensive techniques to implement a computationally universal set of logic gates. Again, we do not have such techniques for the 2D surface code and its variants, and require expensive magic state distillation techniques. While the overhead cost of magic state distillation has been reduced over the years, it is still far from ideal and research continues into improving the distillation process and into discovering new approaches and/or codes that do not require it. In order to avoid the overhead of magic state distillation in the medium term, we envision error mitigation and error correction working together to provide universal gate sets by using error correction to remove noise from Clifford gates and error mitigation on the t-gate.19
A recent breakthrough20 result by Benjamin Brown shows how to realize one of the most resource-intensive gates, called the controlled-controlled-Z gate, in a two-dimensional architecture without resorting to magic state distillation. This approach relies on the observation that a 3D version of the surface code enables an easy implementation of a logical CCZ, and then cleverly embeds the 3D surface code into a 2+1-dimensional space-time.
Reducing the large overhead cost for implementing a computationally universal set of logic gates is a key goal of the quantum error correction community and a vital component in the quest for ever larger quantum computing systems.
Looking forward
Quantum computers are real and available to program, but constructing large, reliable quantum computers remains a significant challenge. Extracting the full potential of these systems will likely require major advances in quantum error correction technology. Fortunately, we appear to be entering into another creative period as the community begins to push in new directions with recent advances such as new qLDPC codes that show promise for the future systems.
We’re proud that IBMers have made key contributions to this field, and we are excited to see that IBM is part of this vibrant community. We're confident that — working together as a community of theorists, experimentalists, and engineers — we’ll be able to overcome the challenges that come with engineering quantum hardware. IBM is excited to build toward a future where scalable quantum computing is a reality.
10: Pavel Panteleev and Gleb Kalachev. 2022. Asymptotically good Quantum and locally testable classical LDPC codes. In Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing (STOC 2022). Association for Computing Machinery, New York, NY, USA, 375–388. https://doi.org/10.1145/3519935.3520017
11: N. P. Breuckmann and J. N. Eberhardt, "Balanced Product Quantum Codes," in IEEE Transactions on Information Theory, vol. 67, no. 10, pp. 6653-6674, Oct. 2021, doi: 10.1109/TIT.2021.3097347.
12: Anthony Leverrier, Gilles Zémor. Quantum Tanner codes. arXiv. [Submitted on 28 Feb 2022 (v1), last revised 16 Sep 2022 (this version, v3)] https://doi.org/10.48550/arXiv.2202.13641
13: Shouzhen Gu, Christopher A. Pattison, Eugene Tang. An efficient decoder for a linear distance quantum LDPC code. arXiv. [Submitted on 14 Jun 2022] https://doi.org/10.48550/arXiv.2206.06557
14: Guanyu Zhu, Tomas Jochym-O’Connor, and Arpit Dua. Topological Order, Quantum Codes, and Quantum Computation on Fractal Geometries. PRX Quantum 3, 030338 – Published 15 September 2022 https://link.aps.org/doi/10.1103/PRXQuantum.3.030338
15: Matthew B. Hastings, and Jeongwan Haah. Dynamically Generated Logical Qubits. Quantum 5, 564 (2021). https://doi.org/10.22331/q-2021-10-19-564
16: Craig Gidney, Michael Newman, and Matt McEwen. Benchmarking the Planar Honeycomb Code. Quantum 6, 813 (2022). https://doi.org/10.22331/q-2022-09-21-813
17: Benjamin J. Brown. Conservation laws and quantum error correction: towards a generalised matching decoder. arXiv. [Submitted on 13 Jul 2022] https://arxiv.org/abs/2207.06428
18: Neereja Sundaresan, et al. Matching and maximum likelihood decoding of a multi-round subsystem quantum error correction experiment. arXiv. [Submitted on 14 Mar 2022 (v1), last revised 20 Apr 2022 (this version, v2)] https://doi.org/10.48550/arXiv.2203.07205
19: Christophe Piveteau, David Sutter, Sergey Bravyi, Jay M. Gambetta, and Kristan Temme. Error Mitigation for Universal Gates on Encoded Qubits. Phys. Rev. Lett. 127, 200505 – Published 12 November 2021 https://link.aps.org/doi/10.1103/PhysRevLett.127.200505
20: Benjamin J. Brown. A fault-tolerant non-Clifford gate for the surface code in two dimensions. Science Advances. 22 May 2020. Vol 6, Issue 21 https://doi.org/10.1126/sciadv.aay4929




