Today, the most powerful classical supercomputers in the world aren’t individual devices powered by a single central processing unit (CPU) or graphics processing unit (GPU). Instead, they are what we call high-performance computing (HPC) clusters—hundreds or even thousands of CPUs and GPUs all working together to tackle the world’s most challenging problems. We believe the future of quantum computing will look very similar, and new research shows that future is closer than you may think.
Even as IBM has worked to scale superconducting quantum processing units (QPUs) beyond the 100-qubit and 1,000-qubit barriers, it has become increasingly clear that a multi-QPU approach may be needed to help quantum computing achieve its true potential. Much like today’s classical HPC clusters, we believe the quantum computers of the future will be made up of multiple processors working together to run circuits much too large and complex for any one QPU. Now, with a new paper recently published in Nature, we’ve delivered the world’s first demonstration of an essential milestone in this journey: two connected QPUs working together to execute a circuit beyond the capabilities of either processor alone.
This work represents important progress toward our vision of quantum-centric supercomputing (QCSC), an emerging high-performance computing framework that integrates both quantum and classical compute resources to execute parallelized workloads that would be impossible to explore with classical computing alone. A few weeks ago, we published a blog post highlighting some preliminary examples of how partners like RIKEN and Cleveland Clinic Foundation are already using the QCSC framework to experiment with hybrid quantum-classical computational workloads on today’s classical HPC systems. These projects are just the beginning.
QCSC will require performant software that allows us to easily break complex problems apart so that CPUs, GPUs, and QPUs can work to solve the parts of an algorithm they are best suited to tackle. Even when we break these problems down into their quantum and classical components, we believe the quantum portion of QCSC workloads will likely contain circuits so complex that we’ll only be able to execute them with multiple QPUs working in concert. We call this modular quantum computing.
IBM has spent years laying the groundwork for modular quantum computing with innovations like IBM Quantum System Two, which is capable of housing multiple QPUs, and through efforts to develop performant software for manipulating and partitioning quantum circuits. Our new Nature paper delivers some promising demonstrations of how we can combine tools and methods like dynamic circuits, circuit cutting, and classical links between separate quantum processors to achieve the second part of that equation.
At the same time, our research is about more than just the long-term future of QCSC. It’s also about expanding the range of applications we can explore today with current quantum hardware. In this blog post, we’ll explain how the novel capabilities we’ve developed as part of this research represent a significant increase in the scale of systems we can simulate with today’s quantum hardware. Before we explore those near-term implications, however, let’s first take a closer look at how our research team used these capabilities to wield two quantum processors as one, and to make progress toward the modular quantum-centric supercomputing frameworks of the future.
How two QPUs become one
In our experiments, we combined two 127-qubit IBM Quantum Eagle processors into a single QPU by connecting them in real-time over a classical link. We then leveraged error-mitigated dynamic circuits and a technique known as circuit cutting to create quantum states comprising up to 142 qubits—i.e., quantum states larger than either Eagle QPU could achieve on its own. Our research is the first experimental demonstration showing that these methods can allow us to execute two-qubit gates even between qubits situated on separate QPUs, a crucial capability in modular quantum computing architectures.
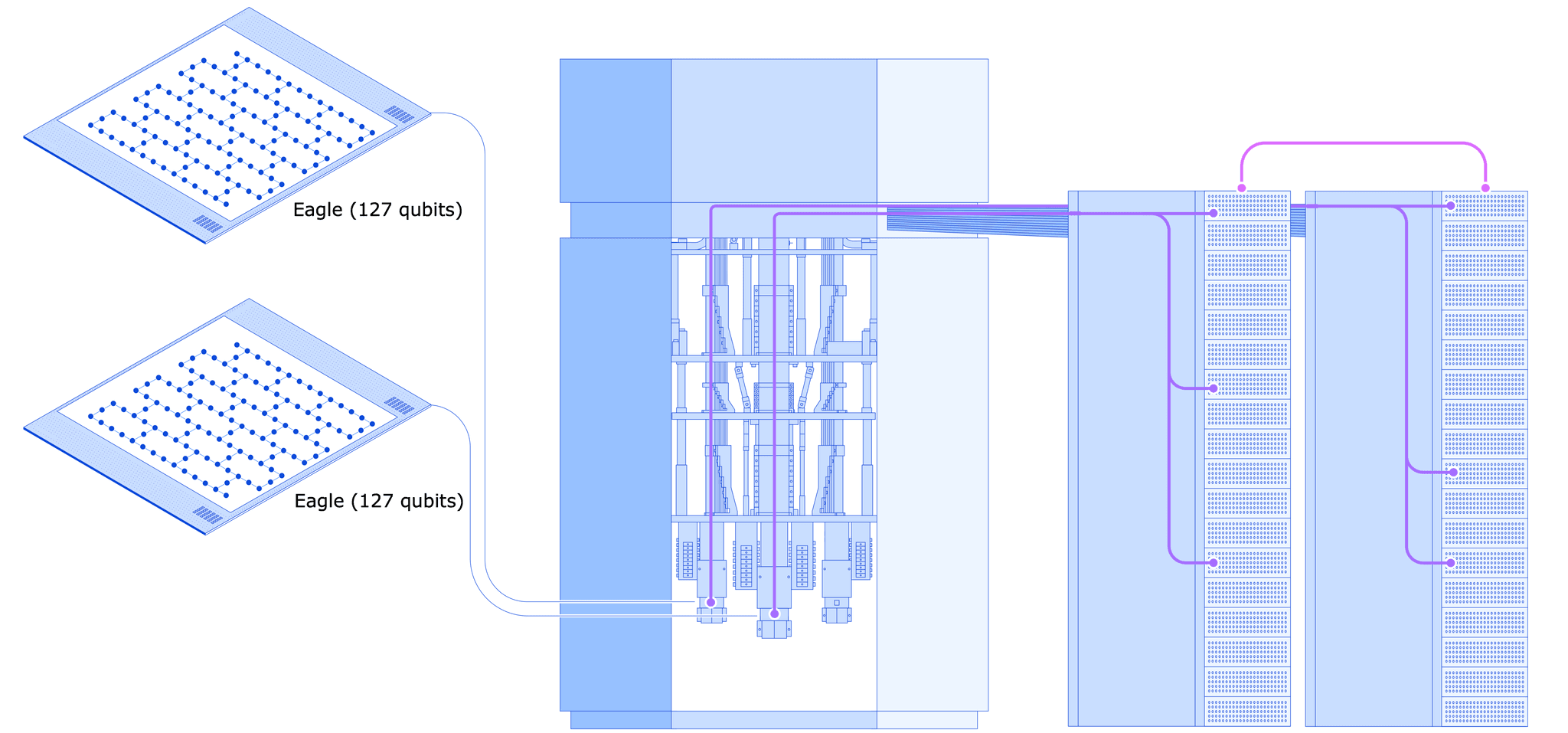
This diagram shows two IBM Quantum Eagle processors connected with a real-time classical link in an IBM Quantum System Two. Each QPU is controlled by its own rack of classical electronics, and the two racks must be tightly synchronized to operate both QPUs as one.
So, how does this work? Let’s start with circuit cutting. When we’re faced with a quantum circuit that’s too large to run on one QPU, we use circuit cutting to decompose it into smaller subcircuits that an individual QPU can handle. We then use classical computation to take the results of these subcircuit runs and join them together, ultimately yielding the result we would have obtained from running the original circuit on a single processor.
It’s worth noting that we don’t actually need two connected QPUs operating on the subcircuits simultaneously to achieve this. We could also run the subcircuits on a single QPU, one after the other, and then combine the results with classical post-processing. The recent Nature paper explores both of these approaches by comparing two different circuit cutting schemes—one based only on local operations (LO) in a single QPU, and another based on a combination of local operations and classical communication (LOCC) between two connected QPUs. More on that later.
In either case, one of the biggest challenges in circuit cutting has to do with two-qubit gates, logical operations we use to entangle and manipulate pairs of qubits. Two-qubit gates are one of the biggest drivers of computational complexity in quantum circuits. Even when we use circuit cutting to break complex circuits into more manageable subcircuits, we still need methods for executing two-qubit gates between qubits in separate subcircuits. In the LOCC scheme, this means we need methods for forming quantum entanglements—or something equivalent—between qubits on separate processors, which are connected only by a classical communications channel.
Using dynamic circuits to build virtual two-qubit gates across two QPUs
Of course, there’s one big challenge when it comes to creating quantum entanglement across a communications channel that transmits only classical information: it’s impossible.
Instead, we used what are called virtual gates to reproduce the statistics of entanglement between qubits on separate processors. More specifically, we created a teleportation circuit that consumes virtual Bell pairs to create the necessary two qubit gates. Bell pairs are a fundamental form of two-qubit entanglement, and virtual Bell pairs are similar. However, instead of implementing genuine quantum entanglement between two qubits, virtual Bell pairs recreate the statistics of entanglement through multiple circuit executions.
Normally, creating Bell pairs between qubits on separate chips would require a long-range CNOT gate connecting the two qubits. CNOT gates are an essential quantum logic operation that we use to create Bell pairs. However, as we’ve established, we cannot perform quantum operations over a classical communications channel. To get around this limitation, we use a quasi-probability decomposition (QPD) over our local operations to recreate the statistics of entanglement, and this yields the “cut” Bell pairs that the teleportation circuit consumes.
Creating the desired quantum state across two QPUs requires consuming multiple cut bell pairs in a teleportation circuit, which we were able to run by tightly synchronizing the quantum circuits on the two connected QPUs. The cut Bell pairs are generated in a "cut Bell pair factory," which you can see illustrated in the green boxes in the figures below:
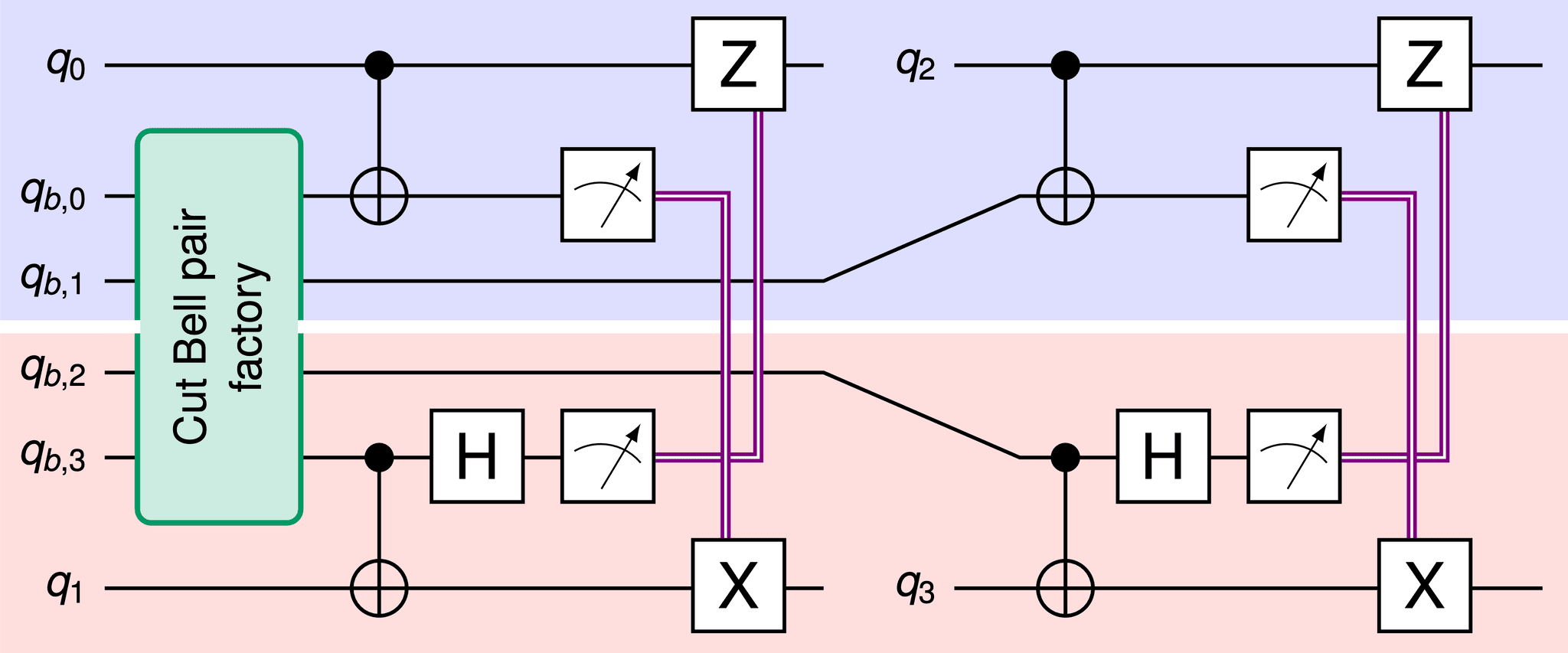
Figure 1b from the Nature paper
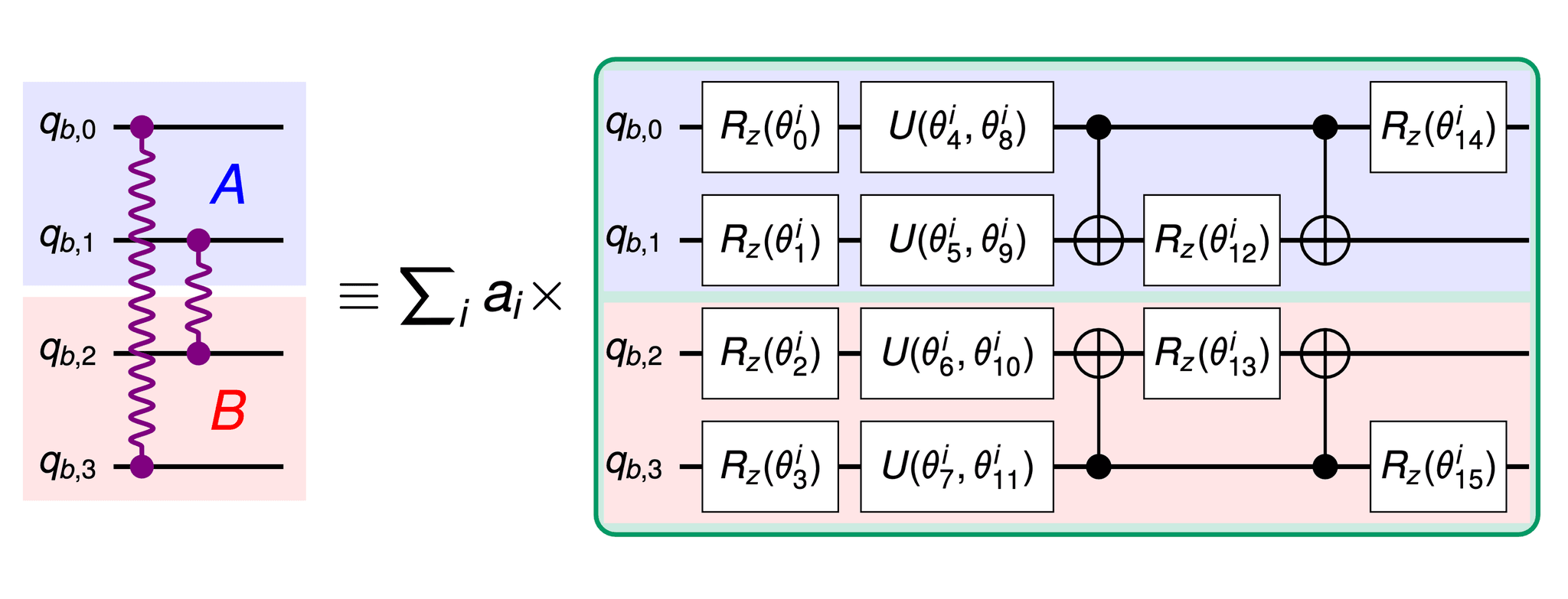
Figure 1c from the Nature paper
These two figures depict the teleportation protocol that makes it possible to entangle qubits on separate QPUs. In each image, the top blue-shaded region represents the portion of the cut Bell pair factory that runs on one QPU, while the bottom red-shaded region represents the portion that runs on the other. Together, the blue- and red-shaded regions illustrate how you can use the protocol to create a CNOT gate connecting qubit 0 (q0) seen at the top of Figure 1b with qubit 1 (q1) at the bottom, and another two-qubit gate connecting qubit 2 (q2) with qubit 3 (q3).
Let’s look at the q0 and q1 example in Figure 1b. We start by creating local CNOT gates between the qubits of interest and secondary qubits located on each of their respective QPUs—in this case connecting q0 with qb,0 and q1 with qb,3. A CNOT gate always consists of a control qubit and a target qubit, so if we use q1 as the control qubit in its local Bell pair, then we’ll need to use q0 as the target in its local bell pair.
We then use dynamic circuits to perform a mid-circuit measurement on the two secondary qubits—qb,0 and qb,3. Dynamic circuits
One challenge with using dynamic circuits is that other qubits in the system must sit idle while the classical computer performs a mid-circuit measurement and calculates the correct operation to perform based on the outcome of that measurement. Idling qubits have a habit of accumulating errors during this delay period due to qubit crosstalk, T1 and T2 decays in the qubit state, and other reasons. This posed a major problem for our experiments.
To overcome this challenge, we developed a novel error mitigation strategy inspired by established error handling methods like zero-noise extrapolation, where noise is amplified so that you can extrapolate back to a zero-noise output, and a common error suppression method called dynamical decoupling. In our method, we insert dynamical decoupling into the delays to suppress some of the errors, and then stretch the delays by multiple factors, which allows us to extrapolate back to the zero-delay state.
This method proved to be surprisingly simple to implement, and it’s likely that future capabilities may make this approach even more efficient, since IBM is currently working to shorten the delays caused by mid-circuit measurement. We believe our new error mitigation method will be useful for a variety of dynamic circuit applications even beyond what we’ve explored in this work.
Before we take those mid-circuit measurements, we apply a Hadamard gate to the secondary qubit that serves as the target in the local Bell pair. We then perform the mid-circuit measurements on the two secondary qubits, obtaining a classical output, and transmit that output across the classical communication link—represented in the figure above by double purple lines—to the primary qubit located on the other QPU.
That’s one circuit run. From there, we repeat this entire process multiple times, running the circuit with different parameters to ultimately recreate the entanglement statistics of a true Bell pair. Quantum researchers have long speculated that this approach should work in theory, but our new paper is among the first to identify the specific quasi-probability decompositions needed to identify these parameters and execute the appropriate circuits on real quantum hardware.
Do we really need connected QPUs?
Connecting two QPUs and operating them as one through LOCC is a significant achievement. It represents what we believe to be the very first experimental realizations of a fundamental concept the quantum research community has talked about for a long time. However, this is just one piece of what we accomplished with this research.
As mentioned above, we also explored an LO-only circuit cutting scheme. In the LO scheme, we still take a large quantum circuit and decompose it into smaller subcircuits that we can run on an individual QPU. However, rather than running the circuits in tight synchronization across two connected QPUs, we can instead run the circuits whenever and wherever we see fit. This means we can run them on separate QPUs with no connection linking them together, or we can run them one after the other on a single QPU.
Both circuit schemes have their advantages and disadvantages. Implementation of LOCC, for example, has a much lower computational cost in terms of the number of samples (i.e. circuit executions) required compared to the LO scheme we tested. It also has a lower cost in the execution pipeline in terms of circuit compilation, since—unlike the LO scheme—LOCC only requires one template circuit that you compile just once. These lower computational costs mean that LOCC is generally much faster than LO.
The LO scheme, by contrast, tends to deliver better quality than LOCC. That’s because the circuits it requires are much simpler, and there’s no need to use dynamic circuits which introduce additional sources of error. There’s also, of course, no classical communication required.
It’s unclear whether one approach will ultimately prove superior to the other. On the one hand, performance improvements in the quantum hardware and software stacks could eventually make the computational cost savings of LOCC irrelevant. On the other hand, this new research has already yielded important learnings about dynamic circuits and quantum circuit compilation that could vastly improve the quality of LOCC. Eventually, researchers hope to develop effective quantum communications links that make sharing entanglement between separate QPUs significantly easier. This is something IBM is already working on with the l-couplers in IBM Quantum Flamingo, which we debuted at the IBM Quantum Developer Conference last month.
Important progress toward QCSC and quantum advantage
We may not know whether LO or LOCC is the superior circuit cutting scheme, but we do know that either method has the potential to enable potentially groundbreaking quantum computing applications, even today.
Our research isn’t just about making incremental progress toward the quantum-centric supercomputing architectures of the future, it’s also about extending the scale and scope of the applications we can explore with the current generation quantum technology. The novel capabilities demonstrated in this work do exactly that.
In our research, we used both LO and LOCC to build a 134-node quantum graph state with periodic boundary conditions on 142 qubits, using Eagle processors with just 127 qubits each. In other words, we were able to take the 2-dimensional heavy-hex lattice of qubits in an Eagle processor, and use circuit cutting to essentially shape that flat lattice into a 3-dimensional cylinder that folds in on itself. This would be impossible to achieve without circuit cutting.
We can see this system illustrated in the figure below, where each purple dot represents a qubit, and each line represents interactions between neighboring qubits. The lines in blue are the periodic boundary conditions created with circuit cutting that allow us to simulate this 3-dimensional shape with a 2-dimensional system.
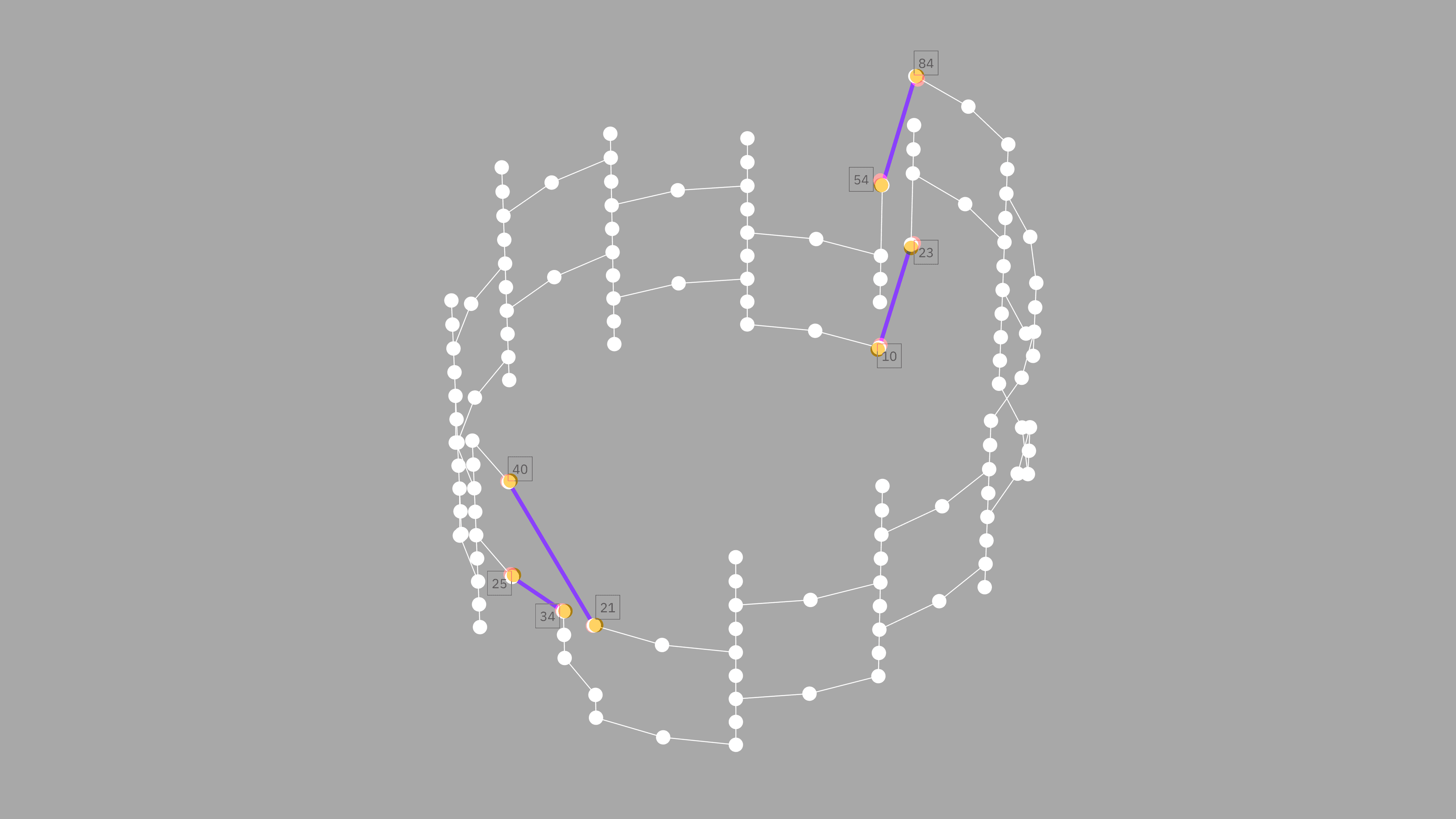
Graph state with periodic boundary conditions
Periodic boundary conditions like these figure prominently in simulations of nature. Researchers use them to approximate the conditions of large or effectively infinite quantum systems, creating a lattice that quantum information can travel around in an endless loop—just like the excitations that make up some atomic system may travel through the endless vacuum of space. Our research significantly expands the scale of the natural systems we can simulate in this paradigm, and these capabilities are relevant to applications beyond the simulation of natural systems—such as quantum error correction and many others.
This is a remarkable step forward in our ability to build quantum states on quantum hardware, and it shows that today’s 100+ qubit QPUs are capable of building simulations beyond the limitations of individual processor qubit counts. We hope that other researchers in the quantum community will soon be able to make use of the capabilities we’ve demonstrated in this paper to explore systems that were previously inaccessible to quantum computation.
For more details on our research, be sure to read the full paper in Nature.




