Geometrías

Según el diccionario revisado Webster de la lengua inglesa, la geometría es la Rama de las matemáticas que investiga las relaciones, propiedades y mediciones de los cuerpos sólidos, superficies, líneas y ángulos; la ciencia que trata de las propiedades y relaciones de magnitudes; la ciencia de las relaciones del espacio. La palabra geometría también se ha utilizado para denotar las funciones geométricas utilizadas durante más de un siglo por los cartógrafos para trazar mapas del mundo. Según esta nueva acepción, una definición abstracta de geometría sería: punto o agregado de puntos que representa un elemento geográfico de la tierra.

En Spatial Extender, el modelo puede expresarse en términos de coordenadas de la característica. El modelo expresa información: por ejemplo, las coordenadas identifican la posición del elemento geográfico con respecto a puntos fijos de referencia. Además, el modelo se puede utilizar para generar información; por ejemplo, la función ST_Overlaps puede utilizar como datos de entrada las coordenadas de dos regiones próximas y notificar como información si las regiones se solapan o no.

Las coordenadas que un elemento geográfico representa se consideran propiedades de la geometría. Algunos tipos de geometrías tienen también otras propiedades; por ejemplo, área, longitud y perímetro.

Las geometrías soportadas por Spatial Extender forman una jerarquía, que se muestra en la siguiente figura. La jerarquía de la geometría está definida por el documento OpenGIS Simple Features Specification for SQL de OpenGIS Consortium, Inc. (OGC). Se pueden crear instancias para siete miembros de la jerarquía. Es decir, se pueden definir con valores de coordenadas específicos y representarse visualmente tal como se muestra en la figura.

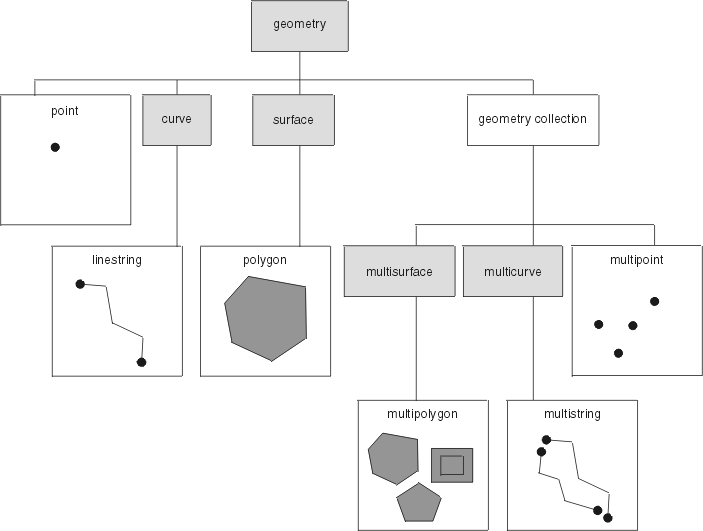
Los tipos de datos espaciales soportados por Spatial Extender son implementaciones de las geometrías mostradas en la figura.

Tal como indica la indica la figura, una superclase denominada geometría es la raíz de la jerarquía. Del tipo raíz y de otros subtipos adecuados de la jerarquía no pueden crearse instancias. Además, los usuarios pueden definir sus propios subtipos adecuados instanciables o no instanciables.

Los subtipos se dividen en dos categorías: los subtipos de geometrías base y los subtipos de colección homogénea.

Tal como sus nombres indican, las colecciones homogéneas son colecciones de geometrías base. Además de tener las propiedades de las geometrías base, las colecciones homogéneas tienen también algunas propiedades propias.